مشکل احتمال برد حین بازی، شناخت احتمال وقوع برد یک تیم در یک نقطه مشخص از بازی، بر طبق آن‌چه که در گذشته و در موقعیت‌های مشابه اتفاق افتاده، است.
این یک ابزار آماری شناخته‌شده در بیسبال، بسکتبال و فوتبال آمریکایی و پرکاربرد در داستان‌گویی‌های ورزشی، آنالیز عملکرد بازیکن و ارزیابی تصمیم‌های گروه مربی‌گری است. هرچند، این یک مفهوم نسبتا جدید در فوتبال به شمار می‌رود.
ما بر این باوریم که این عدم توجه قبلی، نه به علت کمبود داده یا علاقه، بلکه به علت چالش‌های تاکتیکی موجود در این زمینه است. محاسبه پیش‌بینی برد در فوتبال، از مواردی به شمار می‌رود که از لحاظ مفهومی بسیار ساده به نظر می‌رسد، ولی در عمل بسیار چالش برانگیز است.
ما به تازگی مطلبی را در سایت KDD منتشر کرده‌ایم که اشاره به این چالش‌ها دارد! در این مقاله، ما علت‌هایی که این کار را به مشکلی چالش برانگیز تبدیل می‌کنند را بررسی می‌کنیم، یک بررسی اجمالی درباره روش‌هایمان خواهیم داشت و بحث خواهیم کرد که چگونه این مدل می‌تواند برای پیشرفت تجربه تماشاگران یا آنالیز عملکرد بازیکنان تحت فشار ذهنی، مورد استفاده قرار بگیرد.
احتمال برد حین بازی چیست؟
برای درک بهتر احتمال برد حین بازی، روز آخر لیگ برتر فصل ۲۰۱۱/۱۲ را در نظر بگیرید، جایی که منچستر سیتی برای پیروزی در لیگ نیاز به برد داشت.
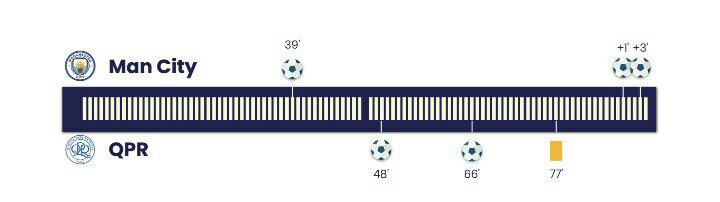
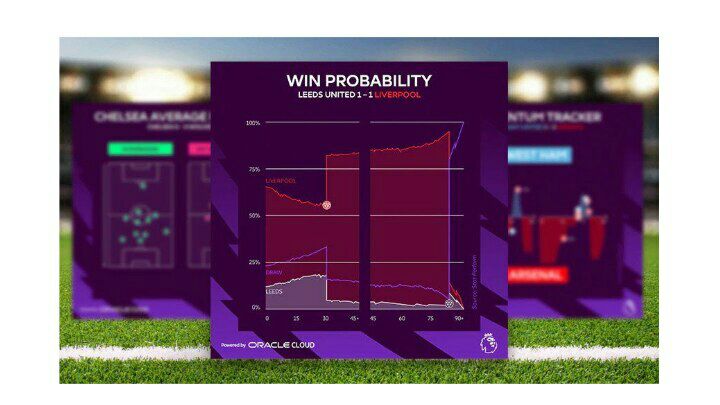
سیتی تا قبل از وقت‌های اضافه نیمه دوم، یک گل از کویینز پارک رنجرز عقب بود، ولی در انتها موفق به کسب پیروزی شد. تصویر زیر که خروجی مدل احتمال برد حین بازی ما است؛ به صورت گرافیکی روند دراماتیک این بازی را دقیقه به دقیقه با احتمال برد/مساوی/باخت به تصویر می‌کشد.
این تصویر نشان می‌دهد که چگونه سیتی با احتمال برد ۸۰ درصد، بازی را به عنوان شانس اصلی برد آغاز کرد، ولی بعد از دقیقه ۶۶ که QPR جلو افتاد به مشکل بزرگی دچار شد، و در دقایق اضافه نفس‌گیر انتهای بازی موفق به بردن حریف شد.
نکته مهمی که باید در نظر داشته باشیم؛ این است که این احتمال‌های برد حین بازی، یک میانگین در بازه‌ای طولانی هستند، پس یک احتمال برد ۲۷ درصدی ضرورتا به این معنا نیست که احتمال واقعی در لحظه ۲۷ درصد است.
این مدل به عنوان مثال، این‌که بازیکنی موقعیت خوب گلزنی در لحظه‌ای از بازی داشته باشد را محاسبه نمی‌کند. این عاملی است که این مدل را از مدل‌های EPV (و نمودارهای جریان بازی) متمایز می‌کند، مدل‌هایی که مکررا امکان گلزنی در سراسر بازی را آپدیت می‌کنند.
تشریح حالت بازی
در مفهوم، ساخت یک مدل احتمال برد حین بازی، امری ساده است. تمام کاری که باید برای یافتن احتمال‌های یک موقعیت انجام گیرد، این است که تمام موقعیت‌های مشابه طی پنج سال گذشته، یا چیزی در آن حدود، را پیدا کنیم و سپس درصد برد تیم‌هایی که در آن موقعیت حضور داشته‌اند را بیابیم.
بنابراین، یکی از اولین تصمیم‌هایی که باید گرفته شود این است که چگونه باید موقعیت فعلی را تشریح کرد، یا ساده‌تر، شاخص‌های این مدل چه هستند.
مدل ما شامل سه دسته از شاخص‌ها می‌شود:
شاخص‌های قدرت تیم، شاخص‌های پایه و شاخص‌های زمینه‌ای. شاخص‌های قدرت تیم، موقعیت پیش از بازی از لحاظ قدرت پیش‌بینی‌شده هر تیم را تشریح می‌کند. آن‌ها به خصوص در زمینه داشتن پیش‌بینی‌های دقیق در اوایل بازی مهم هستند.
شاخص‌های پایه و زمینه‌ای، شاخص‌هایی هستند که در موقعیت حین بازی مورد استفاده قرار می‌گیرند. شاخص‌های پایه، شامل زمان باقی‌مانده از بازی و تفاضل نتیجه فعلی هستند.
این‌ها شاخص‌های اصلی هرگونه مدل احتمال حین برد بازی هستند. شاخص‌های زمینه‌ای بیان‌گر این‌که کدام تیم مومنتوم بازی را در اختیار دارد، هستند.
شاخص‌های قدرت تیم
- رده‌بندی تفاضل: تفاضل در رده‌بندی الو (Elo ratings) بین دو تیم، که تفاوت از قبل تعیین‌شده در قدرت با حریف را بیان می‌کند.
- مزیت ورزشگاه خانگی: این‌که آیا تیم در خانه بازی می‌کند یا خیر.
شاخص‌های پایه:
- زمان بازی: درصد طی‌شده از زمان بازی.
- تفاضل نتیجه: نتیجه فعلی بازی.
شاخص‌های زمینه‌ای:
- گل‌های تیم: تعداد گل‌هایی که تا به الان به ثمر رسیده است.
- کارت‌های قرمز: تفاوت با تیم حریف در تعداد کارت قرمزهای دریافتی.
- کارت‌های زرد: تعداد کارت‌های زرد دریافتی حریف.
- موقعیت‌های گلزنی: تعداد موقعیت‌های گلزنی‌ای که تیم تا به الان ساخته است. این موقعیت‌ها شامل شوت‌های موفق، شوت‌های دفع‌شده و موقعیت‌هایی که در آن بازیکن در شرایط خوبی برای گلزنی بوده را شامل می‌شود.
- پاس‌های هجومی: تعداد پاس‌های هجومی موفق (پاس رو به جلویی که به یک سوم پایانی زمین ارسال می‌شود) در ده دقیقه آخر.
- تهدید موردانتظار (xT): xT یک تیم در ۱۲ دقیقه آخر.
- قدرت دوئل: درصد دوئل‌های پیروزشده در ده دقیقه آخر.
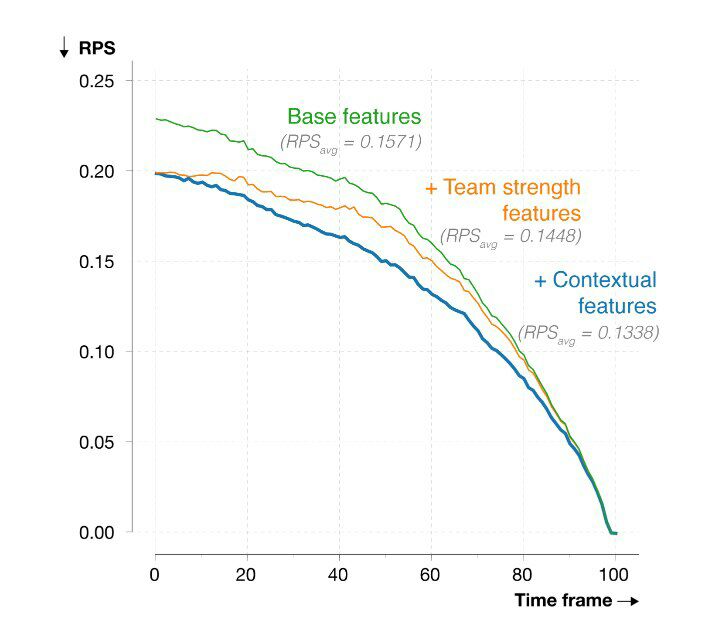
اضافه شدن شاخص‌های زمینه‌ای، مدل ما را بسیار دقیق‌تر می‌کند (همان‌طور که در تصویر زیر قابل مشاهده است)، ولی در عین حال امکان رویکرد مستقیم و ساده را از ما می‌گیرد.
با ارائه‌ای از حالت یک بازی بسیار فشرده، احتمالا بازه‌های زمانی‌ای که تیم میزبان به سمت بردن یا به تساوی کشیدن بازی پیش رفته است، قابل مشاهده خواهد بود.
هرچند که تعداد حالت‌های ممکن بازی در ارائه‌ی ما بسیار بالا است، این امکان وجود دارد که ارائه فعلی به اندازه کافی در گذشته رخ نداده باشد تا احتمال دقیق برد، قابل محاسبه باشد.
یک رویکرد بیزی
در نگاه اول، این هنوز شبیه به یک مشکل سنتی یادگیری ماشینی است. هرچند، ما به سرعت فهمیدیم که این‌گونه نیست.
در ابتدا، زمان محدود بازی‌ها یک رابطه غیرخطی می‌سازد، مخصوصا در حین نزدیک شدن به انتهای بازی. یک برتری مشخص، با جلو رفتن زمان بازی قطعی‌تر می‌شود، و به مرور غیرقابل‌جبران‌تر می‌شود، تا جایی که یک برتری یک گله در انتهای زمان بازی به طور کلی، به اندازه یک برتری پنج گله، قطعی است.
به طور مشابه، هزینه یک کارت قرمز در ابتدای بازی، بیشتر از یک کارت مشابه در ادامه بازی است. با الهام گرفتن از رویکردهای قبلی در بسکتبال و فوتبال آمریکایی، ما این مشکل را با امتحان مدل‌های مختلف برای بخش‌های مختلف بازی حل کردیم.
ما هر نیمه را به ۵۰ فریم زمان تقسیم کردیم، که هر کدام به عنوان یک درصد از بازی ایفای نقش کنند (یا تقریبا یک دقیقه).
هرچند، امتحان مدلی جداگانه برای هرکدام از این فریم‌ها به سادگی مشکل جدیدی را تولید می‌کند.
از آن‌جایی که هر مدل حالا بخش کوچکی از بازی را هدف قرار می‌دهد، داده‌های از پیش یافته‌شده‌ی کم‌تری در دسترس خواهد بود، که ممکن است برآوردهای غیردقیق و یک بی‌ثباتی گسترده در پیش‌بینی از طریق فریم‌های متوالی را به همراه داشته باشد.
برای به تصویر کشیدن این امر، بازی فصل گذشته منچستر یونایتد در مقابل ساندرلند را به خاطر بیاورید. یانکویتز پس از فقط ۲ دقیقه از زمین بازی اخراج شد، امری که وقوع آن در چنین دقیقه‌ای از بازی بسیار نادر است.
بنابراین، این مدل داده‌های کافی برای برآورد احتمالات دقیق در این موقعیت را ندارد. به شکلی کلی‌تر، پیش‌برد تک به تک فریم‌های زمان می‌تواند منجر به پرش‌های ناگهانی در احتمال برد بین روند متوالی فریم‌های زمانی بشود، حتی اگر شرایط بازی چندان تغییر نیافته باشد.
راه حل ما این است تا مدل‌ها را در فریم‌های زمانی متوالی، با استفاده از یک فرایند تصادفی زمانی، در کنار هم قرار بدهیم. زاویه دید فرایند تصادفی، اجازه به اشتراک گذاشتن اطلاعات بین فریم‌های زمانی را می‌دهد.
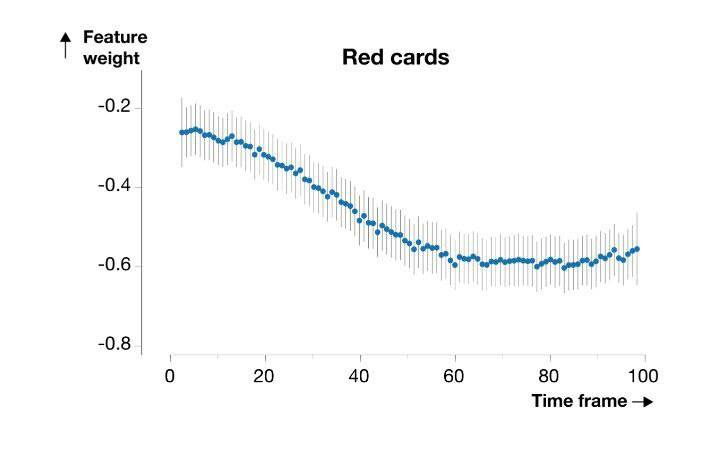
هر مدل اجازه دارد تا فقط مقدار کمی از فریم‌های در همسایگی خودش منحرف بشود. همان‌طور که در تصویر پایین قابل مشاهده است، حالا وزن‌های هر شاخص در طول زمان بازی به تدریج تغییر پیدا می‌کند.
غیرمنتظره نیست که مدل ما آموخته است که یک کارت قرمز، اگر در اوایل بازی رخ دهد جریمه سنگین‌تری در بر خواهد داشت.
طبیعت کم گل بودن فوتبال و وقوع متناوب نتیجه تساوی، یک لایه دیگر از پیچیدگی را اضافه می‌کند. عدم اطمینان موجود در بازی، به علت مقدار زیاد شانس موجود در حاشیه‌های معمولا محدود که تیم‌ها را از یک دیگر جدا می‌کند، آموختن یک دسته‌بندی کننده‌ی دقیق را سخت‌تر می‌کند.
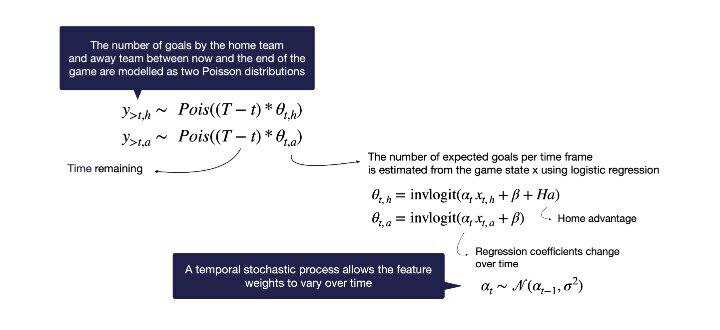
به همین علت، به جای پیش‌بینی مستقیم نتیجه برد/مساوی/باخت، ما تعداد گل‌هایی که یک تیم در ادامه به ثمر خواهند رساند را مدل‌سازی می‌کنیم و سپس، آن را با احتمال برد/مساوی/باخت تطبیق می‌دهیم.
مدل هر فریم زمانی درست مانند پیش‌بینی قبل از بازی کار می‌کند. در هر لحظه‌ای از بازی، این مدل تعداد گل‌هایی که انتظار می‌رود هر تیم در زمان باقی‌مانده به ثمر برساند را با مدل رگرسیون پواسون (Poisson regression) محاسبه می‌کند.
در هر فریم زمان، ما یک ماتریس از تمام نتیجه‌های ممکن در زمان باقی‌مانده از بازی می‌سازیم. هنگامی که ماتریس با نتیجه فعلی بازی ترکیب می‌شود، ما می‌توانیم از آن برای محسابه احتمال برد حین بازی استفاده کنیم.
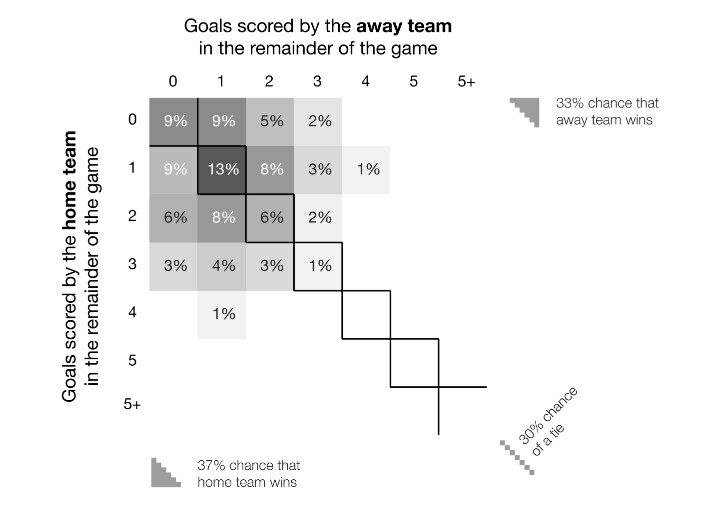چیزی که این رویکرد را بسیار موثر می‌کند، این است که چگونه صراحتا دو فاکتوری که بیشترین تاثیر روی احتمال برد حین بازی دارند را تعریف می‌کند (مدت زمان باقی‌مانده و نتیجه فعلی).
برای ترکیب تمام این ایده‌ها در یک مدل ظریف، ما آن را در یک برنامه بیزی (Bayesian) اجرا کردیم. این برنامه، ایده‌های فوق را به عنوان یک دسته از توزیع‌های ریاضی‌گونه، بیان می‌کند.
با استنتاج متغیر از مشتق‌گیری خودکار (Automatic Differentiation Variational Inference) یا ADVI ما پارامترهای این توزیع‌ها را از داده‌های گذشته نتیجه می‌گیریم.
مزیت دیگر نمونه‌ی بیزی، این است که این روش به صورت طبیعی عدم اطمینان پیش‌بینی‌ها را می‌گیرد.
گاهی اوقات، یک بازی به قدری خاص است که تقریبا هیچ بازی دیگری در گشذته وجود ندارد که نسبت به آن مقایسه شود، که در نتیجه برآوردهای احتمال برد غیردقیقی را به همراه خواهد داشت.
به شکل تصادفی، همچنین نوعی از بازی‌ها وجود دارند که نمودارهای احتمال برد حین بازی در آن‌ها، بیشترین توجه و نقد را دریافت می‌کنند. همچنین عدم قطعیت این مدل می‌تواند برای اطمینان حاصل کردن از مدل‌های احتمال برد مورد استفاده قرار بگیرد.
تجربه هواداران
احتمال برد حین بازی، یک «آمار داستانی» کامل است، به این خاطر که محتوای تاریخی را برای لحظات مشخصی در حین بازی فراهم می‌کند و روند بازی را آشکار می‌کند.
ما در گذشته از آن برای هدفمان در یادداشتی در مورد لیگ حرفه‌ای فصل ۲۰۱۹/۲۰ بلژیک و فینال لیگ قهرمانان ۲۰۲۰ استفاده کرده بودیم.
بعد از بازی، این به ما می‌گوید که کدام لحظات در بازی بیشترین تاثیر را روی برد هر تیم داشته‌اند و همچنین به شما می‌گوید که چقدر امکان داشته تا تیم شکست‌خورده به بازی برگردد و در کدام لحظات این امر ممکن بوده است.
در بیسبال، بسکتبال و فوتبال آمریکایی، این به بخش اصلی مرکز مسابقات ESPN تبدیل شده است.
مانند همیشه، فوتبال از چیزهایی که از سه سال قبل به جریان افتاده‌اند، عقب مانده است.اولین باری که احتمال برد حین بازی را در فوتبال دیدیم، مربوط به برنامه ویژه جام جهانی ۲۰۱۸ سایت ۵۳۸ (five thirty eight) بود.
تقریبا در همان زمان، گوگل شروع به نمایش دادن ویژگی لایوی کرد، اگر یک بازی در حال انجام را گوگل می‌کردید، آمار اوپتا در همکاری با سرویس ویدئویی آمازون در اواخر سال ۲۰۱۹ احتمالات لحظه‌ای در حین بازی را به نمایش می‌گذاشت.
اخیرا، آنالیز آمریکایی فوتبال (American soccer analysis) مدل جدیدی از احتمال برد حین بازی را، بر طبق بعضی از ایده‌های تحقیقات ما، ارائه کرده است. در انتها، با شروع این فصل، لیگ برتر برای پخش احتمال برد حین بازی در پخش زنده، با اوراکل همکاری خواهد کرد.
مختصرا، احتمال برد حین بازی، پیوسته در حال پیدا کردن راه خود در فوتبال به عنوان ابزاری برای بهبود تجربه هواداران است.
فشار روانی
دیگر کاربرد جذاب احتمال برد حین بازی، توانایی شناخت حیاتی‌ترین لحظات بازی است، این می‌تواند به عنوان موقعیت‌هایی که به ثمر رساندن و یا دریافت گل تاثیر بزرگی روی خروجی بازی داشته باشند نیز شناخته شود.
این گروه جدیدی از شاخص‌ها برای اندازه‌گیری عملکرد «حیاتی» (clutch) را فراهم می‌کند. آنالیزورهای فوتبال گاها روی جنبه‌های تکنیکی و گاهی اوقات روی جنبه‌های تاکتیکی تمرکز می‌کنند، ولی جنبه‌های روانی توجهی که لایقش هستند را دریافت نمی‌کنند.
مقایسه چگونگی عملکرد بازیکنان تحت درجه‌های مختلف فشار ذهنی، موضوع مفاله ما در MIT Sloan 2019 و مورد استفاده اصلی مدل احتمال برد حین بازی ما است.
در آن مقاله، ما یک مدل فشار قبل از بازی را با مدل احتمال برد حین بازی خود ترکیب کردیم تا مقدار فشار در هر موقعیت از بازی را بسنجیم. سپس، ما ارزش‌های VAEP به همراه تصمیم‌گیری و اجرای بازیکنان در موقعیت‌های با فشار بالا، متوسط و پایین را با هم مقایسه کردیم.
جان مولر (John Muller) خبرنامه فوق‌العاده‌ای در رباطه با یکی از ایده‌های ما نوشته است، ایده این‌که نیمار تحت فشار نوعا خفه می‌شود.
در این پست، ما مباحث را ساده نگه می‌داریم و نشان می‌دهیم که چگونه احتمال برد حین بازی می‌تواند برای یافتن گلزنان شرایط «حیاتی» یا بازیکن‌هایی که توانسته‌اند تحت فشار روانی بالا گلزنی کنند، مورد استفاده قرار بگیرد.
به همین دلیل، ما شاخص ارزش گل اضافه‌شده (Added goal value) یا به اختصار AGV را طرح می‌کنیم.
این شاخص مجموع ارزش‌های اضافه‌شده در زمینه احتمال برد که از هر کدام از گل‌های یک بازیکن به وقوع پیوسته‌اند را محاسبه کرده، و آن را تقسیم بر تعداد بازی‌های انجام‌شده می‌کند.
از آن‌جایی که هم برد و هم تساوی می‌توانند در فوتبال به عنوان نتیجه موفق ارزیابی شوند، ما این شاخص را به صورت حاصل جمع تغییرات در احتمال برد بازی ضربدر سه به علاوه تغییر در احتمال مساوی بازی محاسبه می‌کنیم.
این نتیجه می‌تواند به عنوان تاثیر میانگین روی امتیازات پیش‌بینی‌شده در لیگ که تیمی در هر بازی توسط گل‌های یک بازیکن به آن می‌رسد، تفسیر بشود.
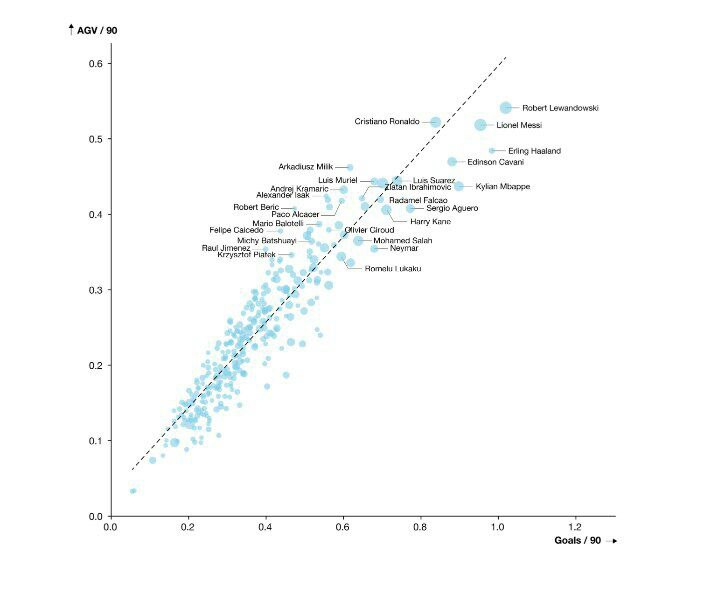
با نگاه به بازیکنانی که حداقل ۲۰ گل در پنج لیگ معتبر اروپایی بین سال‌های ۲۰۱۶/۱۷ تا ۲۰۲۰/۲۱ به ثمر رسانده‌اند، ما متوجه شدیم که لواندوفسکی، رونالدو، مسی، هالند و کاوانی بازیکن‌هایی هستند که بیشترین AGV به ازای هر ۹۰ دقیقه را به ثبت رسانده‌اند و به همین دلیل بیشترین ارزش را با گل‌های خود به جا گذاشته‌اند.
نکته دیگری که جالب توجه است، رابطه بین گل به ازای هر ۹۰ دقیقه و AGV به ازای هر ۹۰ دقیقه است. نمودار قطری زیر، میانگین AGV به ازای هر ۹۰ دقیقه برای بازیکنانی با خروجی هجومی مشابه را به تصویر کشیده است.
بازیکنان زیر این خط مثل نیمار، لواندوفسکی و کاوانی نسبتا ارزش اضافه‌شده به ازاری هر گل پایین‌تری دارند. در حالی که بازیکنان بالای این خط مثل رونالدو، ابراهیموویچ و میلیچ ارزش اضافه‌شده به ازای هر گل بیشتیر نسبت به یک بازیکن متوسط به ثبت رسانده‌اند.
منبع: kuleuven.be
مترجم: نیما نباتی
کاری از گروه فنی آنالیزتاکتیکی
-
دوره تخصصی آنالیز فوتبال (بخش اول)۱,۹۷۰,۰۰۰تومان -
نرم افزار آنالیز گرافیکی۲,۵۸۰,۰۰۰تومان -
دوره آموزش آنالیز فوتبال۱,۰۸۰,۰۰۰تومان